Oma likums visai ķēdei un ķēdes posmam: formulas, apraksta un skaidrojuma rakstīšanas iespējas

Profesionāls elektriķis vai elektronikas speciālists savās darbībās nevar apiet Ohma likumu, risinot problēmas, kas saistītas ar elektronisko un elektrisko ķēžu uzstādīšanu, regulēšanu un remontu.

Patiesībā ikvienam ir jāsaprot šis likums. Jo ar elektrību ikdienā nākas saskarties ikvienam.

Un, lai gan vācu fiziķa Oma likums ir paredzēts vidusskolas mācību programmā, praksē tas ne vienmēr tiek apgūts savlaicīgi. Tāpēc mūsu materiālā mēs apsvērsim tik aktuālu tēmu dzīvei un sapratīsim formulas rakstīšanas iespējas.

Viena sekcija un pilnīga elektriskā ķēde

Apsverot elektrisko ķēdi no Ohma likuma piemērošanas ķēdei, jāņem vērā divas iespējamās aprēķina iespējas: atsevišķai sadaļai un pilnvērtīgai ķēdei.

Elektriskās ķēdes posma strāvas aprēķins

Elektriskās ķēdes daļa, kā likums, tiek uzskatīta par ķēdes daļu, kas izslēdz EML avotu, jo tai ir papildu iekšējā pretestība.

Tāpēc aprēķina formula šajā gadījumā izskatās vienkārša:

I = U/R,

Kur attiecīgi:

• es – strāvas stiprums;
• U – pielietotais spriegums;
• R - pretestība.

Formulas interpretācija ir vienkārša - strāva, kas plūst caur noteiktu ķēdes posmu, ir proporcionāla tai pievadītajam spriegumam, un pretestība ir apgriezti proporcionāla.

Tā sauktā grafiskā "margrietiņa", caur kuru tiek parādīts viss formulējumu variantu kopums, pamatojoties uz Oma likumu. Ērts rīks kabatas uzglabāšanai: sektors “P” - jaudas formulas; sektors “U” - sprieguma formulas; sektors “I” - pašreizējās formulas; sektors “R” - pretestības formulas

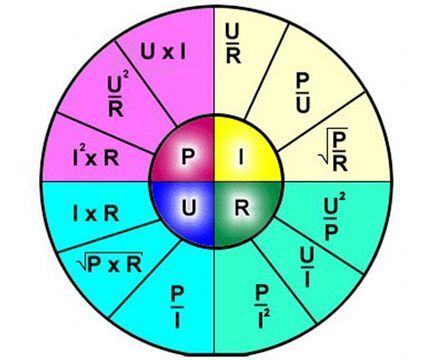
Tādējādi formula skaidri apraksta strāvas plūsmas atkarību caur atsevišķu elektriskās ķēdes sadaļu attiecībā pret noteiktām sprieguma un pretestības vērtībām.

Formulu ir ērti izmantot, piemēram, aprēķinot pretestības parametrus, kas jāielodē ķēdē, ja ir norādīts spriegums un strāva.

Oma likums un divas sekas, kas jāzina ikvienam profesionālam elektromehāniķim, elektroinženierim, elektronikas inženierim un ikvienam, kas iesaistīts elektrisko ķēžu darbībā. No kreisās uz labo: 1 - strāvas noteikšana; 2 - pretestības noteikšana; 3 - sprieguma definīcija, kur I - strāva, U - spriegums, R - pretestība

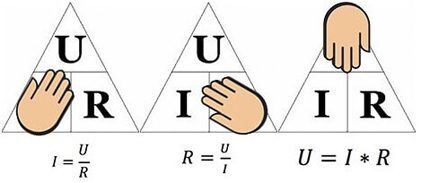
Iepriekš minētais skaitlis palīdzēs noteikt, piemēram, strāvu, kas plūst caur 10 omu pretestību, kurai tiek pielikts 12 voltu spriegums. Aizvietojot vērtības, mēs atrodam – I = 12 / 10 = 1,2 ampēri.

Līdzīgi tiek risinātas problēmas ar pretestības (ja ir zināma strāva un spriegums) vai sprieguma (kad ir zināma spriegums un strāva) atrašanas problēmas.

Tādējādi jūs vienmēr varat izvēlēties nepieciešamo darba spriegumu, nepieciešamo strāvas stiprumu un optimālo pretestības elementu.

Piedāvātā formula neprasa ņemt vērā sprieguma avota parametrus.Tomēr ķēde, kurā ir, piemēram, akumulators, tiks aprēķināta, izmantojot citu formulu. Diagrammā: A – ampērmetra ieslēgšana; V – ieslēdz voltmetru.

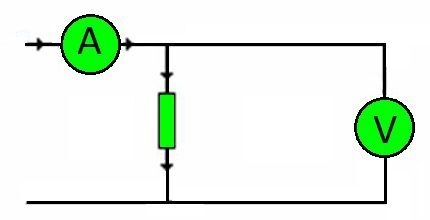
Starp citu, jebkuras ķēdes savienojošie vadi ir pretestības. Slodzes apjomu, kas tiem jāiztur, nosaka spriegums.

Attiecīgi, atkal izmantojot Oma likumu, kļūst iespējams precīzi izvēlēties nepieciešamo vadītāja šķērsgriezumu atkarībā no serdes materiāla.

Mūsu vietnē ir detalizēti norādījumi kabeļa šķērsgriezuma aprēķins jaudas un strāvas ziņā.

Aprēķinu iespēja visai ķēdei

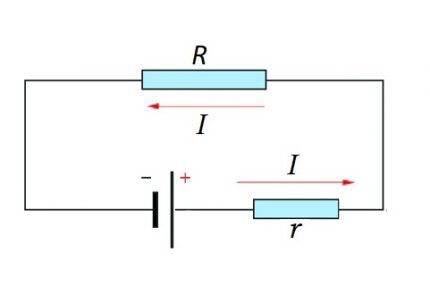
Pilnīga ķēde sastāv no sadaļas (sekcijām), kā arī no EML avota. Tas ir, faktiski EML avota iekšējā pretestība tiek pievienota esošajam ķēdes sekcijas pretestības komponentam.

Tāpēc ir loģiski nedaudz mainīt iepriekš minēto formulu:

I = U / (R + r)

Protams, EML iekšējās pretestības vērtību Ohma likumā visai elektriskajai ķēdei var uzskatīt par nenozīmīgu, lai gan šī pretestības vērtība lielā mērā ir atkarīga no EML avota struktūras.

Tomēr, aprēķinot sarežģītas elektroniskās shēmas, elektriskās ķēdes ar daudziem vadītājiem, papildu pretestības klātbūtne ir svarīgs faktors.

Veicot aprēķinus pilnīgas elektriskās ķēdes apstākļos, vienmēr tiek ņemta vērā EML avota pretestības vērtība. Šī vērtība tiek summēta ar pašas elektriskās ķēdes pretestību. Diagrammā: I - strāvas plūsma; R — ārējais pretestības elements; r ir EML (enerģijas avota) pretestības faktors

Gan ķēdes posmam, gan pilnai ķēdei jāņem vērā dabiskais moments - pastāvīgas vai mainīgas strāvas izmantošana.

Ja iepriekš minētie punkti, kas raksturīgi Ohma likumam, tika ņemti vērā no līdzstrāvas izmantošanas viedokļa, attiecīgi ar maiņstrāvu viss izskatās nedaudz savādāk.

Apsvērums par likuma ietekmi uz mainīgu lielumu

Jēdziens “pretestība” maiņstrāvas caurlaides apstākļiem vairāk jāuzskata par jēdzienu “pretestība”. Tas attiecas uz pretestības slodzes (Ra) un reaktīvās pretestības slodzes (Rr) kombināciju.

Šādas parādības izraisa induktīvo elementu parametri un pārslēgšanas likumi attiecībā pret mainīgu sprieguma vērtību - sinusoidālu strāvas vērtību.

Šī ir līdzvērtīga maiņstrāvas elektriskās ķēdes shēma aprēķiniem, izmantojot formulējumus, kuru pamatā ir Ohma likuma principi: R - pretestības komponents; C ir kapacitatīvā sastāvdaļa; L — induktīvā sastāvdaļa; EML ir enerģijas avots; I - strāvas plūsma

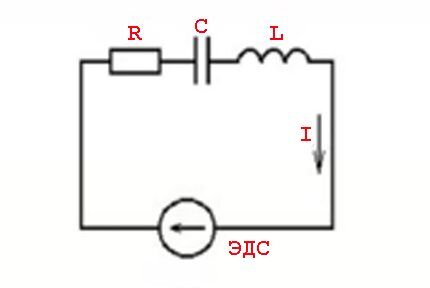
Citiem vārdiem sakot, pastāv strāvas vērtību ietekme, kas noved pie sprieguma vērtībām, ko pavada aktīvās (rezistīvās) un reaktīvās (induktīvās vai kapacitatīvās) jaudas parādīšanās.

Šādas parādības aprēķina pēc formulas:

Z=U/I vai Z = R + J * (X_L -X_C)

Kur: Z - pretestība; R – aktīvā slodze; X_L , X_C – induktīvā un kapacitatīvā slodze; Dž - koeficients.

Elementu sērijveida un paralēlais savienojums

Elektriskās ķēdes elementiem (ķēdes sadaļai) raksturīgs punkts ir seriālais vai paralēlais savienojums.

Attiecīgi katram savienojuma veidam ir pievienots atšķirīgs strāvas plūsmas un sprieguma padeves modelis.Šajā sakarā Ohma likums tiek piemērots arī atšķirīgi atkarībā no elementu iekļaušanas iespējas.

Sērijveidā savienotu pretestības elementu ķēde

Attiecībā uz virknes savienojumu (ķēdes sadaļa ar diviem komponentiem) tiek izmantots šāds formulējums:

• es = es₁ =I₂ ;
• U = U₁ +U₂ ;
• R = R₁ + R₂

Šis formulējums skaidri parāda, ka neatkarīgi no virknē savienoto pretestības komponentu skaita strāva, kas plūst caur ķēdes posmu, nemainās vērtībā.

Pretestības elementu savienošana ķēdes daļā virknē viens ar otru. Šai opcijai ir savs aprēķinu likums. Diagrammā: I, I1, I2 - strāvas plūsma; R1, R2 - pretestības elementi; U, U1, U2 - pielietotais spriegums

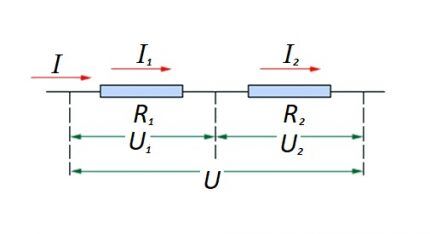
Sprieguma lielums, kas tiek pielietots ķēdes efektīvajiem pretestības komponentiem, ir emf avota summa un kopējā vērtība.

Šajā gadījumā katra atsevišķa komponenta spriegums ir vienāds ar: Ux = I * Rx.

Kopējā pretestība jāuzskata par visu ķēdes pretestības komponentu vērtību summu.

Paralēli savienotu pretestības elementu ķēde

Gadījumā, ja ir paralēls pretestības komponentu savienojums, šāds formulējums tiek uzskatīts par taisnīgu attiecībā uz vācu fiziķa Oma likumu:

• es = es₁ +I₂ … ;
• U = U₁ =U₂ … ;
• 1/R = 1/R₁ + 1/R₂ + …

Nav izslēgtas iespējas izveidot “jaukta” tipa ķēdes posmus, ja tiek izmantoti paralēlie un seriālie savienojumi.

Pretestības elementu savienošana ķēdes posmā paralēli viens otram. Šim variantam tiek piemērots cits aprēķinu likums. Diagrammā: I, I1, I2 - strāvas plūsma; R1, R2 - pretestības elementi; U ir piegādātais spriegums; A, B - ieejas/izejas punkti

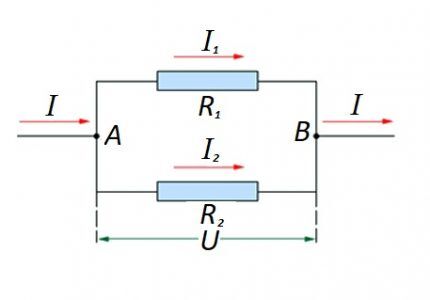
Šādām opcijām aprēķinu parasti veic, sākotnēji aprēķinot paralēlā savienojuma pretestību. Pēc tam iegūtajam rezultātam tiek pievienota virknē savienotā rezistora vērtība.

Likuma integrālās un diferenciālās formas

Visi iepriekš minētie punkti ar aprēķiniem ir piemērojami apstākļiem, kad elektriskās ķēdēs tiek izmantoti, tā sakot, “viendabīgas” struktūras vadītāji.

Tikmēr praksē bieži nākas saskarties ar shēmu konstruēšanu, kur dažādos posmos mainās vadītāju struktūra. Piemēram, tiek izmantoti vadi ar lielāku šķērsgriezumu vai, gluži pretēji, mazāki, izgatavoti no dažādiem materiāliem.

Lai ņemtu vērā šādas atšķirības, pastāv tā sauktā “diferenciālā-integrālā Ohma likuma” variācija. Bezgalīgi mazam vadītājam strāvas blīvuma līmeni aprēķina atkarībā no sprieguma un vadītspējas vērtības.

Diferenciāla aprēķinam tiek izmantota šāda formula: J = ό * E

Attiecīgi integrāļa aprēķinam formulējums ir šāds: I * R = φ1 – φ2 + έ

Tomēr šie piemēri ir drīzāk tuvāki augstākās matemātikas skolai un netiek faktiski izmantoti vienkārša elektriķa praksē.

Secinājumi un noderīgs video par tēmu

Detalizēta Ohma likuma analīze zemāk esošajā videoklipā palīdzēs beidzot nostiprināt zināšanas šajā virzienā.

Unikāla video nodarbība kvalitatīvi pastiprina teorētisko rakstisko prezentāciju:

Elektriķa darbs vai elektronikas inženiera darbība ir cieši saistīta ar brīžiem, kad reāli ir jāievēro Georga Oma likums. Šie ir daži patiesības veidi, kas jāzina ikvienam profesionālim.

Plašas zināšanas šajā jautājumā nav nepieciešamas – pietiek apgūt trīs galvenās formulējuma variācijas, lai to veiksmīgi pielietotu praksē.

Vai vēlaties papildināt iepriekš minēto materiālu ar vērtīgiem komentāriem vai izteikt savu viedokli? Lūdzu, rakstiet komentārus blokā zem raksta. Ja jums ir kādi jautājumi, nevilcinieties jautāt mūsu ekspertiem.